【矩陣力量：線性代數全彩圖解+微課+Python程式設計】

內容簡介

數據科學和機器學習已經深度融合到我們生活的方方面面，而數學正是開啟未來大門的鑰匙。 不是所有人生來都握有一副好牌，但是掌握“數學+程式設計+機器學習”絕對是王牌。 這一次，學習數學不再是為了考試、分數、升學，而是投資時間、自我實現、面向未來。 為了讓大家學數學、用數學，甚至愛上數學，在創作這套書時，作者儘量克服傳統數學教材的各種弊端，讓大家學習時有興趣、看得懂、有思考、更自信、用得著。

鳶尾花書有三大板塊——程式設計、數學、實踐。 數據科學、機器學習的各種算灋離不開數學，本册《矩陣力量》是“數學”板塊的第2本，主要介紹常用線性代數工具。 任何數學工具想要從一元推廣到多元，比如多元微積分、多元統計，都繞不開線性代數。

《矩陣力量：線性代數全彩圖解+微課+ Python編程》共25章內容，可以歸納為7大板塊：向量、矩陣、向量空間、矩陣分解、微積分、空間幾何、數據。 《矩陣力量：線性代數全彩圖解+微課+ Python編程》在講解線性代數工具時，會穿插介紹其在數據科學和機器學習領域的應用場景，讓大家學以致用。 《矩陣力量：線性代數全彩圖解+微課+ Python編程》讀者群包括所有在工作中應用數學的朋友，尤其適用於初級程式師進階，大學本科數學開竅，高級數據分析師，人工智慧開發者。

作者簡介

薑偉生博士FRM。

勤奮的小鎮做題家，熱愛知識視覺化和開源分享。 自2022年8月開始，在GitHub上開源“鳶尾花書”學習資源，截至2023年6月，已經分享3000多頁PDF、3000多幅向量圖、約1000個程式碼檔案，全球讀者數以萬計。

目錄

緒論1

第1章不止向量7

1.1有數據的地方，必有矩陣8

1.2有矩陣的地方，更有向量10

1.3有向量的地方，就有幾何12

1.4有幾何的地方，皆有空間17

1.5有數據的地方，定有統計20

第2章向量運算23

2.1向量：多面手25

2.2行向量、列向量27

2.3向量長度：模，歐氏距離，L2範數31

2.4加減法：對應位置元素分別相加减35

2.5標量乘法：向量縮放36

2.6向量內積：結果為標量37

2.7向量夾角：反余弦43

2.8余弦相似度和余弦距離45

2.9向量積：結果為向量47

2.10逐項積：對應元素分別相乘50

2.11張量積：張起網格面51

第3章向量範數57

3.1 Lp範數：L2範數的推廣58

3.2 Lp範數和超橢圓的聯系61

3.3 L1範數：旋轉正方形64

3.4 L2範數：正圓66

3.5 L∞範數：正方形69

3.6再談距離度量71

第4章矩陣77

4.1矩陣：一個不平凡的表格79

4.2矩陣形狀：每種形狀都有特殊用途81

4.3基本運算：加减和標量乘法85

4.4廣播原則86

4.5矩陣乘法：線性代數的運算覈心88

4.6兩個視角解剖矩陣乘法90

4.7轉置：繞主對角線鏡像92

4.8矩陣逆：“相當於”除法運算94

4.9迹：主對角元素之和95

4.10逐項積：對應元素相乘97

4.11行列式：將矩陣映射到標量值98

第5章矩陣乘法105

5.1矩陣乘法：形態豐富多樣107

5.2向量和向量107

5.3再聊全1列向量112

5.4矩陣乘向量：線性方程組116

5.5向量乘矩陣乘向量：二次型120

5.6方陣乘方陣：矩陣分解123

5.7對角陣：批量縮放124

5.8置換矩陣：調換元素順序127

5.9矩陣乘向量：映射到一維128

5.10矩陣乘矩陣：映射到多元130

5.11長方陣：奇异值分解、格拉姆矩陣、張量積133

5.12愛因斯坦求和約定136

5.13矩陣乘法的幾個雷區138

第6章分塊矩陣143

6.1分塊矩陣：橫平豎直切豆腐145

6.2矩陣乘法第一視角：標量積展開149

6.3矩陣乘法第二視角：外積展開150

6.4矩陣乘法更多視角：分塊多樣化154

6.5分塊矩陣的逆160

6.6克羅內克積：矩陣張量積160

第7章向量空間165

7.1向量空間：從直角坐標系說起166

7.2給向量空間塗顏色：RGB色卡178

7.3張成空間：線性組合紅、綠、藍三原色179

7.4線性無關：紅色和綠色，調不出青色183

7.5非正交基底：青色、品紅、黃色184

7.6基底轉換：從紅、綠、藍，到青色、品紅、黃色187

第8章幾何變換189

8.1線性變換：線性空間到自身的線性映射191

8.2平移：仿射變換，原點變動195

8.3縮放：對角陣196

8.4旋轉：行列式值為1 200

8.5鏡像：行列式值為負205

8.6投影：降維操作207

8.7再談行列式值：幾何視角208

第9章正交投影215

9.1標量投影：結果為標量217

9.2向量投影：結果為向量218

9.3正交矩陣：一個規範正交基222

9.4規範正交基性質226

9.5再談鏡像：從投影視角229

9.6格拉姆-施密特正交化231

9.7投影視角看回歸233

第10章數據投影241

10.1從一個矩陣乘法運算說起242

10.2二次投影+層層疊加245

10.3二特徵數據投影：標準正交基249

10.4二特徵數據投影：規範正交基254

10.5四特徵數據投影：標準正交基259

10.6四特徵數據投影：規範正交基263

10.7數據正交化269

第11章矩陣分解277

11.1矩陣分解：類似因式分解278

11.2 LU分解：上下三角279

11.3 Cholesky分解：適用於正定矩陣280

11.4 QR分解：正交化282

11.5特徵值分解：刻畫矩陣映射的特徵286

11.6奇异值分解：適用於任何實數矩陣290

第12章Cholesky分解295

12.1 Cholesky分解296

12.2正定矩陣才可以進行Cholesky分解297

12.3幾何角度：開合299

12.4幾何變換：縮放→開合302

12.5推廣到三維空間305

12.6從格拉姆矩陣到相似度矩陣309

第13章特徵值分解313

13.1幾何角度看特徵值分解315

13.2旋轉→縮放→旋轉317

13.3再談行列式值和線性變換320

13.4對角化、譜分解323

13.5聊聊特徵值328

13.6特徵值分解中的複數現象330

第14章深入特徵值分解333

14.1方陣開方334

14.2矩陣指數：幂級數的推廣335

14.3斐波那契數列：求通項式337

14.4馬爾科夫過程的平穩狀態339

14.5瑞利商342

14.6再談橢圓：特徵值分解346

第15章奇异值分解353

15.1幾何視角：旋轉→縮放→旋轉355

15.2不同類型SVD分解359

15.3左奇异向量矩陣U 360

15.4右奇异向量矩陣V 363

15.5兩個視角：投影和數據疊加365

第16章深入奇异值分解369

16.1完全型：U為方陣371

16.2經濟型：S去掉零矩陣，變方陣372

16.3緊湊型：非滿秩373

16.4截斷型：近似374

16.5數據還原：層層疊加375

16.6估計與誤差：截斷型SVD 379

16.7正交投影：數據正交化382

第17章多元函數微分387

17.1偏導：特定方向的變化率388

17.2梯度向量：上山方向392

17.3法向量：垂直於切平面396

17.4方向性微分：函數任意方向的變化率398

17.5泰勒展開：一元到多元402

第18章拉格朗日乘子法407

18.1回顧優化問題408

18.2等式約束條件410

18.3線性等式約束414

18.4非線性等式約束415

18.5不等式約束417

18.6再談特徵值分解：優化視角420

18.7再談SVD：優化視角423

18.8矩陣範數：矩陣→標量，矩陣“大小”426

18.9再談數據正交投影：優化視角428

第19章直線到超平面437

19.1切向量：可以用來定義直線438

19.2法向量：定義直線、平面、超平面441

19.3超平面：一維直線和二維平面的推廣443

19.4平面與梯度向量446

19.5中垂線：用向量求解析式451

19.6用向量計算距離453

第20章再談圓錐曲線457

20.1無處不在的圓錐曲線459

20.2正圓：從組織圓到任意正圓460

20.3組織圓到旋轉橢圓：縮放→旋轉→平移463

20.4多元高斯分佈：矩陣分解、幾何變換、距離468

20.5從組織雙曲線到旋轉雙曲線474

20.6切線：搆造函數，求梯度向量476

20.7法線：法向量垂直於切向量479

第21章曲面和正定性481

21.1正定性483

21.2幾何視角看正定性485

21.3開口朝上抛物面：正定486

第22章數據與統計501

22.1統計+線性代數：以鳶尾花數據為例502

22.2平均值：線性代數視角503

22.3質心：平均值排列成向量505

22.4中心化：平移508

22.5分類數據：加標籤510

22.6方差：平均值向量沒有解釋的部分512

22.7協方差和相關性係數514

22.8協方差矩陣和相關性係數矩陣517

第23章數據空間523

23.1從數據矩陣X說起524

23.2向量空間：從SVD分解角度理解527

23.3緊湊型SVD分解：剔除零空間529

23.4幾何視角說空間532

23.5格拉姆矩陣：向量模、夾角余弦值的集合體537

23.6標準差向量：以數據質心為起點540

23.7白話說空間：以鳶尾花數據為例543

第24章數據分解549

24.1為什麼要分解矩陣？ 550

24.2 QR分解：獲得正交系555

24.3 Cholesky分解：找到列向量的座標557

24.4特徵值分解：獲得行空間和零空間559

24.5 SVD分解：獲得四個空間562

第25章數據應用567

25.1從線性代數到機器學習568

25.2從隨機變數的線性變換說起572

25.3單方向映射574

25.4線性回歸578

25.5多方向映射582

25.6主成分分析584

----------------------------------

【數學要素：全彩圖解+微課+Python程式設計】

編輯推薦

這是一套前所未見的數學書，更是一套具備極高顏值的書。 薑偉生博士自謙“小鎮做題家”，實際上他是國際著名金融企業的金融科技專家。 很難想像一比特以“術數”為業的金融家具備如此徹底的分享動機，同時，薑博士有著卓越的藝術品位和設計能力，不僅承擔了這套書的精深內容，更承擔了全系圖書的整體設計。 希望讀者從枯燥的常規數學書中解脫出來，賞心悅目地慢慢走入繽紛的數學宇宙。

內容簡介

數據科學和機器學習已經深度融合到我們生活的方方面面，而數學正是開啟未來大門的鑰匙。 不是所有人生來都握有一副好牌，但是掌握“數學+程式設計+機器學習”絕對是王牌。 這次，學習數學不再是為了考試、分數、升學，而是投資時間、自我實現、面向未來。 為了讓大家學數學、用數學，甚至愛上數學，在創作這套書時，作者儘量克服傳統數學教材的各種弊端，讓大家學習時有興趣、看得懂、有思考、更自信、用得著。

《數學要素：全彩圖解+微課+ Python編程》打破數學板塊的藩籬，將算數、代數、線性代數、幾何、解析幾何、概率統計、微積分、優化方法等板塊有機結合在一起。 從加、减、乘、除四則運算講起，主要內容包括：第1、2章講解向量和矩陣的基本運算； 第3章講解常用幾何知識； 第4章講解代數知識； 第5、6兩章介紹坐標系； 第7、8、9三章介紹解析幾何； 第10章到第14章都是圍繞函數展開； 第15章到第19章講解微積分以及優化問題內容； 第20、21兩章是概率統計入門； 《數學要素：全彩圖解+微課+ Python編程》最後四章以線性代數收尾。

《數學要素：全彩圖解+微課+ Python編程》內容編排上突出“圖解+程式設計+機器學習應用”。 講解一些特定數學工具時，《數學要素：全彩圖解+微課+ Python編程》會穿插介紹其在數據科學和機器學習領域應用場景，讓大家學以致用。

《數學要素：全彩圖解+微課+ Python編程》雖標榜“從加減乘除到機器學習”，但是建議讀者至少具備高中數學知識。 如果讀者正在學習或曾經學過大學數學（微積分、線性代數、概率統計），就更容易讀了。

作者簡介

薑偉生博士FRM。

勤奮的小鎮做題家，熱愛知識視覺化和開源分享。 自2022年8月開始，在GitHub上開源“鳶尾花書”學習資源，截至2023年4月，已經分享2000多頁PDF、2000多幅向量圖、約1000個程式碼檔案，全球讀者數以萬計。

目錄

緒論1

第1章萬物皆數7

1.1數位和運算：人類思想的偉大飛躍9

1.2數位分類：從複數到自然數11

1.3加减：最基本的數學運算15

1.4向量：數位排成行、列18

1.5矩陣：數位排列成長方形19

1.6矩陣：一組列向量，或一組行向量23

1.7矩陣形狀：每種形狀都有特殊性質和用途25

1.8矩陣加减：形狀相同，對應位置，批量加减26

第2章乘除29

2.1算術乘除：先乘除，後加减，括弧內先算31

2.2向量乘法：標量乘法、向量內積、逐項積34

2.3矩陣乘法：最重要的線性代數運算規則36

2.4矩陣乘法第一視角40

2.5矩陣乘法第二視角43

2.6矩陣除法：計算逆矩陣46

第3章幾何49

3.1幾何緣起：根植大地，求索星空51

3.2點動成線，線動成面，面動成體54

3.3角度和弧度60

3.4畢氏定理到三角函數62

3.5圓周率估算初賽：割圓術64

第4章代數69

4.1代數的前世今生：薪火相傳71

4.2集合：確定的一堆東西72

4.3從代數式到函數75

4.4楊輝三角：代數和幾何的完美合體79

4.5排列組合讓二項式係數更具意義82

4.6楊輝三角隱藏的數位規律85

4.7方程組：求解雞兔同籠問題86

第5章笛卡兒坐標系91

5.1笛卡兒：我思故我在93

5.2坐標系：代數視覺化，幾何參數化94

5.3圖解“雞兔同籠”問題100

5.4極座標：距離和夾角102

5.5參數方程：引入一個參數103

5.6坐標系必須是“橫平豎直的方格”？ 104

第6章三維坐標系107

6.1三維直角坐標系109

6.2空間平面：三元一次方程110

6.3空間直線：三元一次方程組114

6.4不等式：劃定區域117

6.5三大類不等式：約束條件120

6.6三維極座標126

第7章距離131

7.1距離：未必是兩點間最短線段132

7.2歐氏距離：兩點間最短線段134

7.3點到直線的距離140

7.4等距線：換個視角看距離144

7.5距離間的量化關係146

第8章圓錐曲線149

8.1圓錐曲線外傳150

8.2圓錐曲線：對頂圓錐和截面相交152

8.3正圓：特殊的橢圓155

8.4橢圓：機器學習的多面手157

8.5旋轉橢圓：幾何變換的結果160

8.6抛物線：不止是函數164

8.7雙曲線：引力彈弓的軌跡166

第9章深入圓錐曲線169

9.1圓錐曲線：探索星辰大海171

9.2離心率：聯系不同類型圓錐曲線172

9.3一組有趣的圓錐曲線173

9.4特殊橢圓：和給定矩形相切175

9.5超橢圓：和範數有關179

9.6雙曲函數：基於組織雙曲線184

9.7圓錐曲線的一般形式186

第10章函數191

10.1當代數式遇到坐標系193

10.2一元函數：一個引數194

10.3一元函數性質197

10.4二元函數：兩個引數202

10.5降維：二元函數切一刀得到一元函數205

10.6等高線：由函數值相等點連成208

第11章代數函數211

11.1初等函數：數學模型的基礎212

11.2一次函數：一條斜線214

11.3二次函數：一條抛物線218

11.4多項式函數：從疊加角度來看221

11.5冪函數：底數為引數224

11.6分段函數：不連續函數228

第12章超越函數231

12.1指數函數：指數為引數233

12.2對數函數：把連乘變成連加235

12.3高斯函數：高斯分佈之基礎238

12.4邏輯函數：在0和1之間取值240

12.5三角函數：週期函數的代表243

12.6函數變換：平移、縮放、對稱246

第13章二元函數251

13.1二元一次函數：平面253

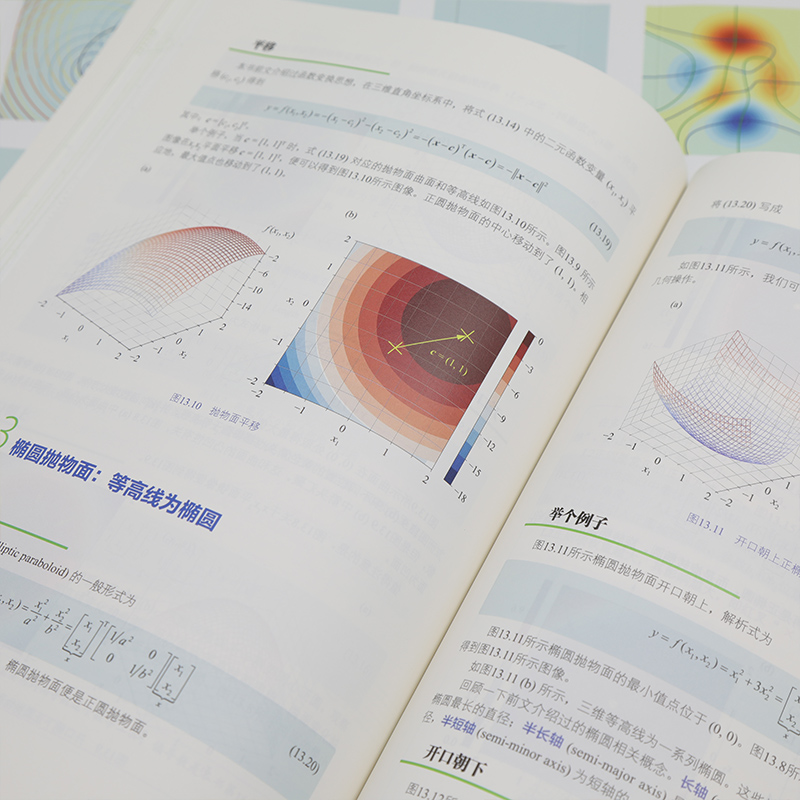
13.2正圓抛物面：等高線為正圓257

13.3橢圓抛物面：等高線為橢圓260

13.4雙曲抛物面：馬鞍面264

13.5山谷和山脊：無數極值點265

13.6錐面：正圓抛物面開方267

13.7絕對值函數：與超橢圓有關269

13.8邏輯函數：從一元到二元272

13.9高斯函數：機器學習的多面手274

第14章數列277

14.1芝諾悖論：阿基裡斯追不上烏龜279

14.2數列分類281

14.3等差數列：相鄰兩項差相等282

14.4等比數列：相鄰兩項比值相等284

14.5斐波那契數列287

14.6累加：大寫西格瑪288

14.7數列極限：微積分的一塊基石299

14.8數列極限估算圓周率301

第15章極限和導數305

15.1牛頓小傳307

15.2極限：研究微積分的重要數學工具308

15.3左極限、右極限310

15.4幾何視角看導數：切線斜率312

15.5導數也是函數315

第16章偏導數323

16.1幾何角度看偏導數325

16.2偏導也是函數329

16.3二階偏導：一階偏導函數的一階偏導330

16.4二元曲面的駐點：一階偏導為0 333

第17章微分337

17.1幾何角度看微分：線性近似338

17.2泰勒級數：多項式函數近似340

17.3多項式近似和誤差343

17.4二元泰勒展開：用多項式曲面近似348

17.5數值微分：估算一階導數352

第18章積分355

18.1萊布尼茨：既生瑜，何生亮357

18.2從小車勻加速直線運動說起357

18.3一元函數積分358

18.4高斯函數積分361

18.5誤差函數：S型函數的一種362

18.6二重積分：類似二重求和363

18.7“偏積分”：類似偏求和365

18.8估算圓周率：牛頓法367

18.9數值積分：黎曼求積371

第19章優化入門377

19.1優化問題：尋找山峰、山谷379

19.2構造優化問題380

19.3約束條件：限定蒐索區域383

19.4一元函數的極值點判定389

19.5二元函數的極值點判定393

第20章概率入門401

20.1概率簡史：出身賭場402

20.2二叉樹：一生二、二生三403

20.3拋硬幣：正反面概率407

20.4聊聊概率：向上還是向下409

20.5一枚質地不均勻的硬幣411

20.6隨機中有規律413

第21章統計入門417

21.1統計的前世今生：強國知十三數418

21.2散點圖：當數據遇到坐標系419

21.3平均值：集中程度421

21.4標準差：離散程度424

21.5協方差：聯合變化程度425

21.6線性相關係數：線性關係强弱429

第22章向量435

22.1向量：有大小、有方向436

22.2幾何視角看向量運算439

22.3向量簡化距離運算441

22.4向量內積與向量夾角443

22.5二維到三維445

22.6投影：影子的長度446

----------------------------

【統計至簡：概率統計全彩圖解+微課+ Python程式設計】

內容簡介

數據科學和機器學習已經深度融合到我們生活的方方面面，而數學正是開啟未來大門的鑰匙。 不是所有人生來都握有一副好牌，但是掌握“數學程式設計機器學習”的知識絕對是王牌。 這一次，學習數學不再是為了考試、分數、升學，而是投資時間、自我實現、面向未來。 為了讓大家學數學、用數學，甚至愛上數學，在創作時，作者儘量克服傳統數學教材的各種弊端，讓大家學習時有興趣、看得懂、有思考、更自信、用得著。

《統計至簡：概率統計全彩圖解微課Python編程》是“鳶尾花數學大系—從加減乘除到機器學習”叢書中數學版塊—“數學三劍客”的第三册，也是最後一本。 “數學”板塊的第一本《數學要素》是各種數學工具的“大雜燴”，可謂數學基礎； 《矩陣力量》專門講解機器學習中常用的線性代數工具； 本册《統計至簡》則介紹機器學習和資料分析中常用的概率統計工具。 《統計至簡：概率統計全彩圖解微課Python編程》的覈心是“多元統計”，離不開第二册《矩陣力量》中介紹的線性代數工具。 《統計至簡：概率統計全彩圖解微課Python編程》內容又可以歸納為7大板塊——統計、概率、高斯、隨機、頻率派、貝葉斯派、橢圓。 《統計至簡：概率統計全彩圖解微課Python編程》在講解概率統計工具時，會穿插介紹其在數據科學和機器學習領域的應用場景，讓大家學以致用。

《統計至簡：概率統計全彩圖解微課Python編程》讀者群包括所有在工作中應用概率統計的朋友，尤其適用於初級程式師進階、大學本科數學開竅、高級數據分析師、機器學習開發者。

作者簡介

薑偉生博士FRM。

勤奮的小鎮做題家，熱愛知識視覺化和開源分享。 自2022年8月開始，在GitHub上開源“鳶尾花書”學習資源，截至2023年9月，已經分享4000多頁PDF、4000多幅向量圖、約2000個程式碼檔案，全球讀者數以萬計。

目錄

緒論1

第1章概率統計全景7

1.1數學工具：一個線性代數小測驗8

1.2統計描述9

1.3概率10

1.4高斯16

1.5隨機19

1.6頻率派19

1.7貝葉斯派20

1.8橢圓三部曲21

第2章統計描述23

2.1統計兩大工具：描述、推斷25

2.2長條圖：單特徵數據分佈26

2.3散點圖：兩特徵數據分佈31

2.4有標籤數據的統計視覺化33

2.5集中度：平均值、質心36

2.6分散度：極差、方差、標準差38

2.7分比特：四分比特、百分比特等40

2.8箱型圖：小提琴圖、分佈散點圖42

2.9中心距：平均值、方差、偏度、峰度44

2.10多元隨機變數關係：協方差矩陣、相關性係數矩陣47

第3章古典概率模型51

3.1無處不在的概率52

3.2古典概率：離散均勻概率律56

3.3回顧：楊輝三角和概率64

3.4事件之間的關係：集合運算65

3.5條件概率：給定部分資訊做推斷67

3.6貝葉斯定理：條件概率、邊緣概率、聯合概率關係70

3.7全概率定理：窮舉法73

3.8獨立、互斥、條件獨立76

第4章離散隨機變數79

4.1隨機：天地不仁，以萬物為芻狗80

4.2期望值：隨機變數的可能取值加權平均89

4.3方差：隨機變數離期望距離平方的平均值91

4.4累積分佈函數（CDF）：累加94

4.5二元離散隨機變數95

4.6協方差、相關性係數97

4.7邊緣概率：偏求和，相當於降維100

4.8條件概率：引入貝葉斯定理101

4.9獨立性：條件概率等於邊緣概率104

4.10以鳶尾花數據為例：不考慮分類標籤107

4.11以鳶尾花數據為例：考慮分類標籤116

4.12再談概率1：展開、折疊120

第5章離散分佈123

5.1概率分佈：高度理想化的數學模型124

5.2離散均勻分佈：不分厚薄125

5.3伯努利分佈：非黑即白128

5.4二項分佈：楊輝三角129

5.5多項分佈：二項分佈推廣132

5.6泊松分布：建模隨機事件的發生次數135

5.7幾何分佈：滴水穿石136

5.8超幾何分佈：不放回138

第6章連續隨機變數141

6.1一元連續隨機變數142

6.2期望、方差和標準差145

6.3二元連續隨機變數147

6.4邊緣概率：二元PDF偏積分149

6.5條件概率：引入貝葉斯定理151

6.6獨立性：比較條件概率和邊緣概率153

6.7以鳶尾花數據為例：不考慮分類標籤154

6.8以鳶尾花數據為例：考慮分類標籤162

第7章連續分佈171

7.1連續均勻分佈：離散均勻分佈的連續版172

7.2高斯分佈：最重要的概率分佈，沒有之一173

7.3邏輯分佈：類似高斯分佈177

7.4學生t-分佈：厚尾分佈179

7.5對數常态分配：源自常态分配181

7.6指數分佈：泊松分布的連續隨機變數版183

7.7卡方分佈：若干IID標準常态分配平方和184

7.8 F-分佈：和兩個服從卡方分佈的獨立隨機變數有關185

7.9 Beta分佈：概率的概率187

7.10 Dirichlet分佈：多元Beta分佈190

第8章條件概率197

8.1離散隨機變數：條件期望198

8.2離散隨機變數：條件方差204

8.3離散隨機變數的條件期望和條件方差：以鳶尾花為例206

8.4連續隨機變數：條件期望215

8.5連續隨機變數：條件方差216

8.6連續隨機變數：以鳶尾花為例217

8.7再談如何分割“1”221

第9章一元高斯分佈231

9.1一元高斯分佈：期望值决定位置，標準差决定形狀232

9.2累積概率密度：對應概率值234

9.3標準高斯分佈：期望為0，標準差為1 236

9.4 68-95-99.7法則239

9.5用一元高斯分佈估計概率密度243

9.6經驗累積分佈函數244

9.7 QQ圖：分比特-分點陣圖245

9.8從距離到一元高斯分佈249

第10章二元高斯分佈253

10.1二元高斯分佈：看見橢圓254

10.2邊緣分佈：一元高斯分佈258

10.3累積分佈函數：概率值262

10.4用橢圓解剖二元高斯分佈264

10.5聊聊線性相關性係數268

10.6以鳶尾花數據為例：不考慮分類標籤272

10.7以鳶尾花數據為例：考慮分類標籤281

第11章多元高斯分佈287

11.1矩陣角度：一元、二元、三元到多元288

11.2高斯分佈：橢圓、橢球、超橢球293

11.3解剖多元高斯分佈PDF 298

11.4平移→旋轉302

11.5平移→旋轉→縮放308

第12章條件高斯分佈311

12.1聯合概率和條件概率關係312

12.2給定X條件下，Y的條件概率：以二元高斯分佈為例316

12.3給定Y條件下，X的條件概率：以二元高斯分佈為例321

12.4多元正態條件分佈：引入矩陣運算325

第13章協方差矩陣331

13.1計算協方差矩陣：描述數據分佈332

13.2相關性係數矩陣：描述Z分數分佈338

13.3特徵值分解：找到旋轉、縮放340

13.4 SVD分解：分解數據矩陣345

13.5 Cholesky分解：列向量座標349

13.6距離：歐氏距離VS馬氏距離350

13.7幾何視角：超橢球、橢球、橢圓353

13.8合併協方差矩陣362

第14章隨機變數的函數367

14.1隨機變數的函數：以鳶尾花為例368

14.2線性變換：投影視角369

14.3單方向投影：以鳶尾花兩特徵為例372

14.4正交系投影：以鳶尾花兩特徵為例376

14.5以橢圓投影為視角看線性變換380

14.6主成分分析：換個視角看數據383

第15章蒙特卡洛類比387

15.1蒙特卡洛類比：基於偽亂數發生器388

15.2估算平方根389

15.3估算積分390

15.4估算體積391

15.5估算圓周率391

15.6布豐投針估算圓周率393

15.7接受-拒絕抽樣法395

15.8二項分佈隨機漫步397

15.9兩個服從高斯分佈的隨機變數相加399

15.10產生滿足特定相關性的亂數400

第16章頻率派統計推斷411

16.1統計推斷：兩大學派412

16.2頻率學派的工具414

16.3中心極限定理：漸近於常态分配416

16.4最大似然：雞兔比例419

16.5最大似然：以估算平均值、方差為例421

16.6區間估計：總體方差已知，平均值估計424

16.7區間估計：總體方差未知，平均值估計427

16.8區間估計：總體平均值未知，方差估計429

第17章概率密度估計431

17.1概率密度估計：從長條圖說起432

17.2核密度估計：若干核函數加權疊合435

17.3頻寬：决定核函數的高矮胖瘦439

17.4核函數：八種常見核函數441

17.5二元KDE：概率密度曲面443

第18章貝葉斯分類447

18.1貝葉斯定理：分類鳶尾花448

18.2似然概率：給定分類條件下的概率密度450

18.3先驗概率：鳶尾花分類占比451

18.4聯合概率：可以作為分類標準451

18.5證據因數：和分類無關452

18.6後驗概率：也是分類的依據453

18.7單一特徵分類：基於KDE 457

18.8單一特徵分類：基於高斯461

第19章貝葉斯分類進階467

19.1似然概率：給定分類條件下的概率密度468

19.2聯合概率：可以作為分類標準470

19.3證據因數：和分類無關472

19.4後驗概率：也是分類的依據474

19.5獨立：不代表條件獨立477

19.6條件獨立：不代表獨立478

第20章貝葉斯推斷入門483

20.1貝葉斯推斷：更貼合人腦思維484

20.2從一元貝葉斯公式說起486

20.3走地雞兔：比例完全不確定488

20.4走地雞兔：很可能一半一半495

20.5走地雞兔：更一般的情况504

第21章貝葉斯推斷進階511

21.1除了雞兔，農場發現了猪512

21.2走地雞兔猪：比例完全不確定517

21.3走地雞兔猪：很可能各1/3 520

21.4走地雞兔猪：更一般的情况525

第22章馬爾可夫鏈蒙特卡洛529

22.1歸一化因數沒有閉式解？ 530

22.2雞兔比例：使用PyMC3 534

22.3雞兔猪比例：使用PyMC3 537

第23章馬氏距離543

23.1馬氏距離：考慮數據分佈的距離度量544

23.2歐氏距離：最基本的距離546

23.3標準化歐氏距離：兩個視角547

23.4馬氏距離：兩個視角549

23.5馬氏距離和卡方分佈553

第24章線性回歸557

24.1再聊線性回歸558

24.2最小二乘法561

24.3優化問題562

24.4投影視角563

24.5線性方程組：代數視角563

24.6條件概率564

24.7最大似然估計（MLE）568

第25章主成分分析571

25.1再聊主成分分析572

25.2原始數據574

25.3特徵值分解協方差矩陣575

25.4投影577

25.5幾何視角看PCA 583

25.6奇异值分解586

25.7優化問題591

25.8數據還原和誤差