



只需要(馬同學圖解微積分下册):點擊書店客服或LINE按鈕與客服聯系
馬同學圖解微積分(下)
作者簡介
馬同學是專業的數學知識內容創作團隊,從2016年起就在公眾號上進行數學內容創作,作品累計數千萬人次觀看,知乎認證數學話題優秀答主,收穫四十餘萬贊。
目錄
第9章向量代數與空間解析幾何
9.1向量及其線性運算
9.1.1從單變數到多變數
9.1.2向量與有向線段·
9.1.3直角坐標系
9.1.4向量的定義
9.1.5零向量·
9.1.6向量的加法
9.1.7向量的數乘
9.1.8向量的減法
9.1.9線性運算的運算規律
9.1.10線性組合和空間平面
9.2數量積(點積)
9.2.1數量積(點積)的定義
9.2.2向量的長度
9.2.3向量的夾角
9.2.4方向角與方向余弦
9.2.5投影·
9.2.6數量積(點積)的運算規律
9.2.7投影的運算規律·
9.2.8平行與正交
9.3向量積(叉積)和混合積
9.3.1二階行列式的幾何意義
9.3.2向量積(叉積)
9.3.3向量積(叉積)的性質
9.3.4混合積·
9.3.5混合積的性質
9.4平面及其方程
9.4.1直線的方向向量·
9.4.2平面的法線和法向量
9.4.3平面的點法式方程
9.4.4平面的一般方程·
9.4.5平面的截距式方程
9.4.6平面的參數方程·
9.4.7兩平面的夾角
9.4.8點到平面的距離·
9.5空間直線及其方程
9.5.1空間直線的一般方程
9.5.2空間直線的點向式方程
9.5.3空間直線的參數方程
9.5.4空間直線的夾角·
9.5.5直線與平面的夾角
9.5.6直線的平面束方程
9.6曲面及其方程
9.6.1球面的方程
9.6.2旋轉曲面
9.6.3柱面·
9.6.4二次曲面
9.7空間曲線及其方程
9.7.1空間曲線的一般方程
9.7.2空間曲線的參數方程
9.7.3曲面的參數方程·
9.7.4座標面上的投影·
第10章多元函數微分法及其應用
10.1多元函數的基本概念
10.1.1平面點集和點集
10.1.2多元函數
10.1.3二元函數的鄰域與去心鄰域
10.1.4內點、外點和邊界點
10.1.5開集和閉集
10.1.6連通集、開區域和閉區域·
10.1.7有界集和無界集
10.2多元函數的極限和連續
10.2.1聚點·
10.2.2多元函數極限的定義
10.2.3多元函數的連續
10.2.4多元函數的間斷
10.3偏導數、偏微分和全微分
10.3.1尋找曲面微分的思路
10.3.2偏微分和偏導數
10.3.3求出全微分
10.3.4偏導數的例題·
10.3.5高階偏導數和混合偏導數·
10.4求出全微分·
10.4.1全微分的定義·
10.4.2全微分的計算·
10.4.3可微分與連續·
10.4.4可微分的充分條件
10.5多元複合函數的求導法則
10.5.1一元函數與二元函數的複合
10.5.2多元函數的複合
10.6微分與雅可比矩陣、行列式·
10.6.1各種微分的共性
10.6.2雅可比矩陣、行列式
10.6.3鏈式法則
10.7隱函數的求導公式·
10.8多元函數微分學的幾何應用·
10.8.1向量函數
10.8.2向量函數的極限
10.8.3向量函數的導數與微分·
10.8.4切線與法平面·
10.8.5法線與切平面·
10.9方向導數與梯度
10.9.1方向導數
10.9.2可微分時的方向導數
10.9.3梯度與方向導數
10.9.4等值線
10.9.5梯度與等值線·
10.10多元函數的極值及其求法·
10.10.1最值和極值
10.10.2函數極值的必要條件
10.10.3函數極值的充分條件
10.11條件極值和拉格朗日乘數法·
10.11.1條件極值
10.11.2可轉為無條件極值的例題
第11章重積分·
11.1二重積分的概念和性質
11.1.1曲頂柱體
11.1.2二重積分的定義
11.1.3二重積分的齊次性與可加性
11.1.4平頂柱體的體積
11.1.5二重積分的區域可加性·
11.1.6二重積分的不等式
11.1.7二重積分估值的不等式·
11.1.8二重積分的中值定理
11.2直角坐標系下的二重積分計算
11.2.1直角坐標系下的二重積分·
11.2.2 X、Y型區域·
11.2.3直角坐標系下的富比尼定理
11.3極坐標系下的二重積分計算·
11.3.1極坐標系下的二重積分·
11.3.2θ型區域
11.3.3極坐標系下的富比尼定理·
11.4各種坐標系下的二重積分計算
11.5三重積分及其計算·
11.5.1三重積分的定義
11.5.2三重積分的富比尼定理·
11.6三重積分的換元法·
11.6.1柱面坐標系
11.6.2球面坐標系
11.7重積分的應用
11.7.1曲面的面積
11.7.2平面質心和空間質心
11.7.3空間中的萬有引力
第12章曲線積分與曲面積分·
12.1對弧長的曲線積分·
12.1.1直線積分
12.1.2對弧長的曲線積分的定義·
12.1.3對弧長的曲線積分的性質·
12.1.4對弧長的曲線積分的計算法
12.2對座標的曲線積分·
12.2.1向量場
12.2.2對座標的曲線積分的定義·
12.2.3對座標的曲線積分的性質·
12.2.4對座標的曲線積分的計算法
12.2.5兩類曲線積分的關係
12.3曲線積分的基本定理
12.3.1從直線積分的基本定理到曲線積分的基本定理
12.3.2重力場與重力勢能
12.3.3保守場及其充要條件
12.3.4與路徑無關的定義
12.3.5保守場以及與路徑無關·
12.3.6本節小結
12.4格林公式·
12.4.1平面積分
12.4.2平面積分的基本定理:格林公式·
12.4.3窗戶上的格林公式
12.4.4格林公式的例題
12.4.5旋度與環流量·
12.4.6保守場無旋
12.5對面積的曲面積分·
12.5.1對面積的曲面積分的定義·
12.5.2對面積的曲面積分的計算法
12.6對座標的曲面積分·
12.6.1有向曲面和不可定向
12.6.2光照強度
12.6.3有向曲面的積分的定義·
12.6.4對座標的曲面積分的定義·
12.6.5對座標的曲面積分的計算法
12.7斯托克斯公式和高斯公式
12.7.1斯托克斯公式·
12.7.2格林公式的改寫
12.7.3高斯公式
12.7.4積分的基本定理
第13章無窮級數
13.1常數項級數的概念和性質
13.1.1等比級數
13.1.2調和級數
13.1.3收斂常數項級數的性質·
13.2正項級數及其審斂法
13.2.1正項級數及其收斂的充要條件
13.2.2正項級數的比較審斂法·
13.2.3正項級數的極限比較審斂法
13.2.4正項級數的比值審斂法·
13.2.5正項級數的根值審斂法·
13.2.6本節小結
13.3交錯級數和絕對收斂
13.3.1交錯級數
13.3.2萊布尼茨審斂法
13.3.3絕對收斂與條件收斂
13.3.4黎曼重排定理·
13.3.5本節小結
13.4幂級數
13.4.1函數項級數
13.4.2幂級數的定義·
13.4.3阿貝爾定理
13.4.4收斂半徑的求解方法
13.5泰勒級數·
13.5.1泰勒級數和泰勒展開式·
13.5.2求解麥克勞林展開式的例題
13.5.3幂級數的加減乘除
13.5.4幂級數的性質·
13.6傅裡葉級數·
13.6.1萬物皆是波
13.6.2傅裡葉級數及其收斂定理·
13.6.3正弦級數和余弦級數
13.6.4一般週期函數的傅裡葉級數
-------------------------------------

【馬同學圖解微積分】
內容簡介
本書通過圖解的形式,在邏輯上穿針引線,講解了大學公共課“高等數學(微積分)”中與單變數函數相關知識點,也就是經典教材《高等數學》上册中的絕大多數知識點。這些知識點是相關專業的在校、考研學生必須掌握的,也是相關從業人員深造所應必備的。本書圍繞著”線性相似”,講解了極限、導數、微分、中值定理、洛必達法則、泰勒公式、極值、最值、定積分、牛頓萊布尼茨公式、微分方程求解等知識,邏輯上層層遞進,再輔以精心挑選的各種例題、生活案例等,大大降低了學習門檻。
作者簡介
馬同學是專業的數學知識內容創作團隊,從2016年起就在公眾號上進行數學內容創作,作品累計數千萬人次觀看,知乎認證數學話題優秀答主,收穫四十餘萬贊。
目錄
第1章引言1
1.1開普勒第二定律1
1.2線性近似的思想2
1.3古典微積分3
1.4古典微積分的問題4
第2章函數與極限6
2.1柯西的數列極限6
2.1.1用數列來表示矩形逼近曲邊梯形這一過程6
2.1.2柯西的數列極限9
2.1.3無窮大符號10
2.1.4阿基裡斯悖論10
2.1.5古典微積分問題的解决12
2.2魏爾斯特拉斯的數列極限13
2.2.1魏爾斯特拉斯的數列極限介紹14
2.2.2數列極限的另外一種定義20
2.3數列極限的性質22
2.3.1數列極限的唯一性23
2.3.2收斂數列的有界性24
2.3.3收斂數列的保號性26
2.3.4收斂數列的子數列27
2.4趨於無窮的函數極限28
2.4.1趨於無窮、正無窮、負無窮的函數極限28
2.4.2無窮極限存在的充要條件34
2.5一般的函數極限35
2.5.1飛矢不動35
2.5.2鄰域、去心鄰域以及一般的函數極限37
2.5.3單側極限41
2.5.4極限存在的充要條件43
2.5.5小結45
2.6無窮小45
2.6.1極限和局部45
2.6.2無窮小的定義和意義47
2.6.3極限與無窮小49
2.7無窮大50
2.7.1正無窮大、負無窮大和無窮大的定義50
2.7.2無窮小與無窮大52
2.8極限的性質54
2.8.1極限的唯一性55
2.8.2極限的局部有界性55
2.8.3極限的局部保號性56
2.9海涅定理59
2.9.1海涅定理的幾何意義60
2.9.2 xn ̸= x0 61
2.9.3海涅定理的例題62
2.10極限的運算法則64
2.10.1無窮小的運算法則64
2.10.2極限的各種運算法則66
2.10.3抛物線下的面積71
2.11夾逼定理72
2.12複合函數的極限78
2.13漸近線84
2.13.1水准漸近線84
2.13.2鉛直漸近線85
2.13.3斜漸近線86
2.14單調有界數列必有極限89
2.14.1單調數列和單調函數89
2.14.2單調有界準則90
2.14.3歐拉數e 90
2.14.4歐拉數e的現實意義93
2.14.5自然底數94
2.14.6歐拉數e的例題95
2.15無窮小的比較95
2.15.1具體的無窮小的比較95
2.15.2等價無窮小96
2.16函數的連續性99
2.16.1連續的定義99
2.16.2左連續、右連續102
2.16.3連續函數102
2.16.4點連續105
2.17函數的間斷點106
2.18連續函數的運算與初等函數的連續性109
2.18.1和、差、積、商的連續性109
2.18.2反函數的連續性110
2.18.3複合函數的連續性111
2.18.4初等函數的連續性113
2.18.5極限求解的例題113
2.19閉區間上連續函數的性質114
2.19.1最值和極值114
2.19.2有界性與最大值最小值定理116
2.19.3零點定理117
2.19.4介值定理117
2.19.5通過極限求出圓的面積119
第3章微分與導數120
3.1微分與線性近似120
3.2通過導數求出微分123
3.2.1微分的定義123
3.2.2導數的定義128
3.2.3左導數、右導數129
3.2.4連續與可導131
3.2.5微分與切線133
3.2.6割線與切線133
3.2.7圓周率等於4 134
3.2.8微分與導數的符號136
3.3常用的一些導函數136
3.4函數和、差、積、商的求導法則140
3.5複合函數的導函數142
3.5.1鏈式法則142
3.5.2關於鏈式法則的常見誤解145
3.6反函數的導函數145
3.7隱函數的導函數149
3.7.1函數、顯函數和隱函數149
3.7.2局部的隱函數151
3.7.3對數求導法153
3.8參數方程的導函數與相關變化率154
3.8.1參數方程的導函數154
3.8.2相關變化率156
3.9高階導數157
3.10小結159
第4章微分中值定理與導數的應用161
4.1微分中值定理161
4.1.1費馬引理和駐點161
4.1.2羅爾中值定理163
4.1.3拉格朗日中值定理166
4.1.4柯西中值定理170
4.1.5微分中值定理的例題174
4.2洛必達法則174
4.2.1未定式176
4.2.2洛必達法則的較弱形式和加强形式177
4.2.3洛必達法則的更多形式180
4.2.4洛必達法則的局限性182
4.3泰勒公式182
4.3.1泰勒定理和皮亞諾餘項183
4.3.2為什麼可以通過多項式來逼近函數f(x)187
4.3.3泰勒公式的係數和餘項189
4.3.4麥克勞林公式191
4.3.5皮亞諾餘項和拉格朗日餘項192
4.3.6泰勒公式的例題193
4.4函數的單調性與凹凸性194
4.4.1導數與函數的單調性194
4.4.2函數的凹凸性197
4.4.3拐點200
4.5函數的極值與最值203
4.5.1極值的充分條件203
4.5.2閉區間上函數的最值207
4.6曲率208
4.6.1圓的曲率209
4.6.2曲線的曲率209
第5章不定積分217
5.1不定積分的概念與性質217
5.1.1原函數217
5.1.2達布定理218
5.1.3不定積分的定義219
5.1.4基本積分表220
5.1.5不定積分的性質221
5.2不定積分的換元法222
5.2.1不定積分的第一類換元法223
5.2.2不定積分的第二類換元法225
5.3分部積分法和有理函數的積分227
5.3.1分部積分法227
5.3.2有理函數的積分229
第6章定積分232
6.1定積分與曲邊梯形232
6.1.1定積分的定義232
6.1.2曲邊梯形及其面積237
6.2定積分的可積條件和性質239
6.2.1可積的充分條件239
6.2.2定積分的補充規定241
6.2.3定積分的齊次性與可加性242
6.2.4定積分的性質243
6.3微積分基本定理247
6.3.1積分上限函數247
6.3.2微積分第一基本定理249
6.3.3微積分第二基本定理250
6.4定積分的換元法和分部積分法253
6.4.1定積分的換元法253
6.4.2定積分的分部積分法256
6.5反常積分256
6.5.1無窮限的反常積分256
6.5.2無界函數的反常積分261
第7章定積分的應用265
7.1定積分與曲線長度265
7.1.1光滑曲線及其長度265
7.1.2圓的曲率269
7.1.3曲線的曲率270
7.2定積分與面積271
7.2.1曲線之間的面積271
7.2.2極坐標系下的面積277
7.3表面積與體積279
7.3.1圓錐面的表面積279
7.3.2圓檯面的表面積280
7.3.3旋轉面的表面積281
7.3.4旋轉體的體積285
7.3.5截面積已知的立體圖形的體積287
7.4定積分在物理中的應用288
7.4.1變力沿直線做功288
7.4.2水壓力290
7.4.3力矩與質心291
7.4.4萬有引力293
第8章微分方程296
8.1微分方程的基本概念296
8.1.1微分方程的定義296
8.1.2解、通解、特解和初值條件300
8.2可分離變數的微分方程300
8.2.1可分離變數的微分方程的定義301
8.2.2可分離變數的微分方程的求解方法301
8.3齊次方程303
8.4一階線性微分方程304
8.4.1一階線性微分方程的求解方法304
8.4.2伯努利微分方程306
8.5可降階的高階微分方程308
8.5.1 y(n)= f(x)型的微分方程308
8.5.2 y= f(x,y)型的微分方程309
8.5.3 y= f(y,y)型的微分方程309
8.6高階線性微分方程309
8.6.1高階線性微分方程的定義310
8.6.2線性方程組解的結構310
8.6.3線性微分方程解的結構311
8.6.4常數變易法313
8.7常係數線性微分方程315
8.7.1二階常係數齊次線性微分方程的解
8.7.2 f(x)= e λ xPm(x)時的常係數非齊次線性微分方程
-------------------------------------------


【馬同學圖解線性代數】
內容簡介
本書通過圖解的形式,在邏輯上穿針引線,講解了大學公共課“線性代數”的相關知識點,也就是經典版本的《線性代數》中的絕大多數知識點。 這些知識點是相關在校學生的必修課程,也是從業人員深造的必要知識。 本書引入了矩陣函數,從函數角度講解了向量空間、線性方程組求解、矩陣的秩、行列式、相似變換、特徵值特徵向量、二次型等知識,邏輯上一以貫之,再輔以很多生活案例,大大降低了學習門檻。
作者簡介
馬同學是專業的數學知識內容創作團隊,從2016年起就在公眾號上進行數學內容創作,作品累計數千萬人次觀看,知乎認證數學話題優秀答主,收穫四十餘萬贊。
目錄
第1章向量空間及其性質1
1.1向量2
1.1.1有向線段2
1.1.2向量的定義3
1.1.3零向量5
1.1.4長度和方向6
1.2向量的加法和數乘6
1.2.1向量的加法6
1.2.2向量的數乘10
1.2.3基本運算法則11
1.3線性組合與線性相關12
1.3.1混合顏色13
1.3.2線性組合15
1.3.3線性相關和線性無關17
1.3.4線性相關和線性無關的例題18
1.3.5昇維與降維20
1.4向量空間21
1.4.1宇宙空間和向量空間22
1.4.2向量空間的嚴格定義23
1.4.3特殊向量空間24
1.4.4子空間25
1.5張成空間26
1.5.1等價向量組28
1.5.2幾何意義31
1.5.3最大無關組33
1.5.4向量組的秩34
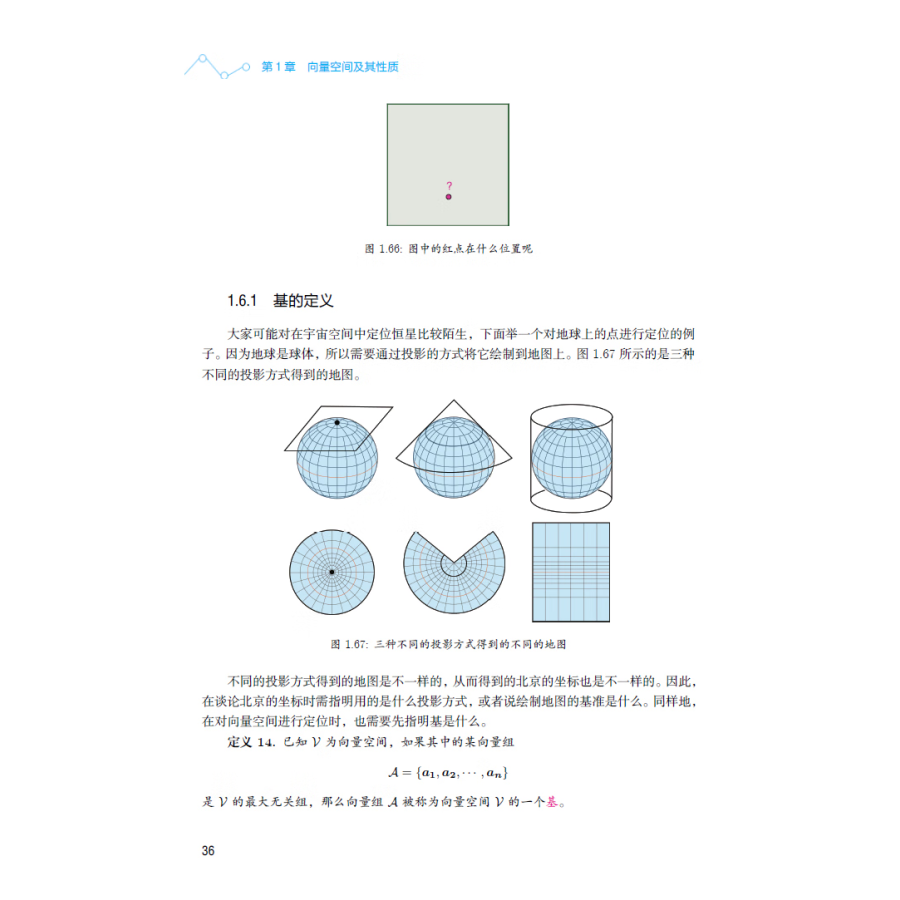
1.6向量空間的基35
1.6.1基的定義36
1.6.2基與座標38
1.6.3坐標系40
1.6.4向量空間的維度42
1.7數量積(點積)43
1.7.1歐氏幾何43
1.7.2長度和角度44
1.7.3新的運算47
1.7.4點積的性質48
1.7.5余弦相似性50
第2章矩陣和矩陣乘法53
2.1矩陣和線性方程組53
2.1.1電視轉播與線性方程組53
2.1.2線性方程組55
2.1.3矩陣的出現56
2.1.4矩陣標記法與解線性方程組58
2.1.5矩陣乘法59
2.1.6矩陣的結合62
2.1.7彩色電視機的計算63
2.2高斯消元法64
2.2.1高斯消元法的思想64
2.2.2特殊矩陣69
2.2.3初等行變換與初等行矩陣72
2.3矩陣的加法與乘法75
2.3.1矩陣加法75
2.3.2矩陣數乘76
2.3.3矩陣乘法的合法性77
2.3.4矩陣乘法的行觀點77
2.3.5矩陣乘法的列觀點78
2.3.6矩陣乘法的點積觀點79
2.3.7矩陣乘法的性質80
2.4矩陣的幂運算與轉置81
2.4.1幂運算81
2.4.2矩陣的轉置83
2.4.3對稱陣與反對稱陣85
2.5矩陣乘法的幾何意義86
2.5.1矩陣的左乘和右乘86
2.5.2矩陣的乘法89
2.5.3總結91
第3章矩陣函數及其幾何意義92
3.1矩陣函數與線性函數92
3.1.1函數92
3.1.2矩陣函數94
3.1.3矩陣是線性函數95
3.2旋轉矩陣函數98
3.2.1旋轉矩陣的左乘98
3.2.2旋轉橢圓99
3.3常用的矩陣函數100
3.3.1組織陣101
3.3.2鏡像矩陣102
3.3.3伸縮矩陣102
3.3.4剪切矩陣103
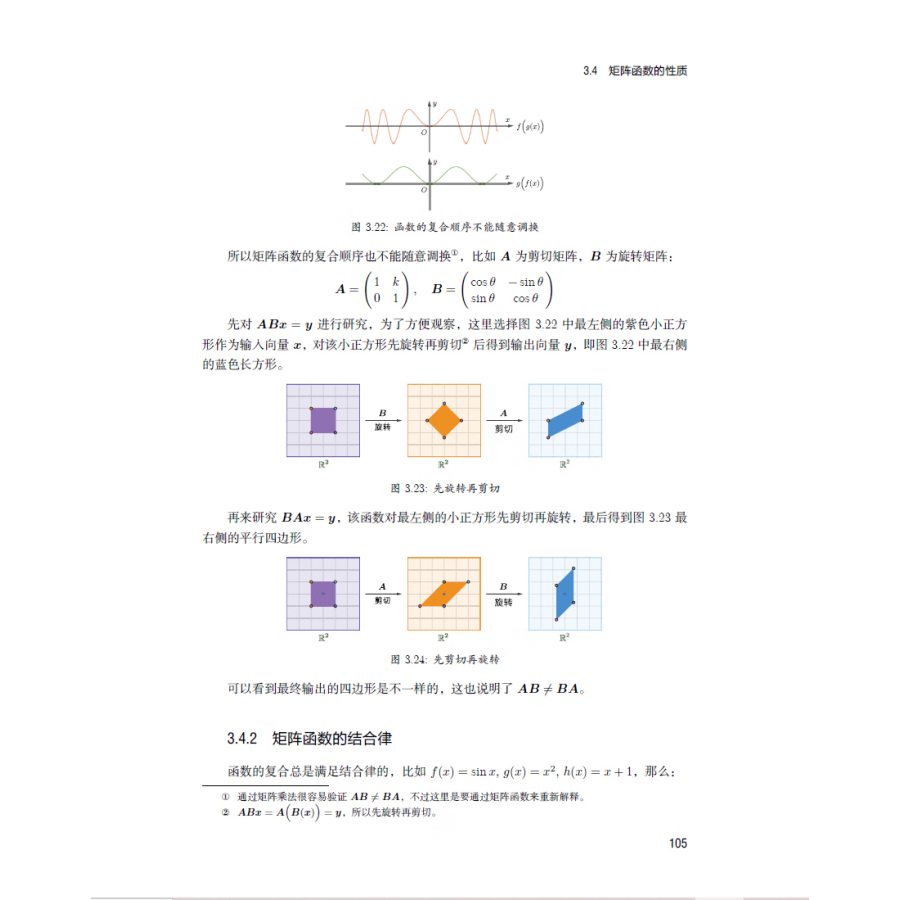
3.4矩陣函數的性質104
3.4.1矩陣函數的交換律104
3.4.2矩陣函數的結合律105
第4章矩陣的秩的定義及意義107
4.1矩陣的秩107
4.1.1列空間107
4.1.2行空間109
4.1.3行秩、列秩、矩陣的秩110
4.2矩陣函數的四要素111
4.2.1定義域112
4.2.2映射法則113
4.2.3值域115
4.2.4到達域115
4.2.5矩陣函數116
4.3矩陣函數的值域117
4.3.1值域與列空間117
4.3.2值域與矩陣的秩119
4.3.3矩陣的秩的性質121
4.4矩陣函數的單射124
4.5矩陣函數的滿射131
4.6矩陣函數的雙射133
4.7逆矩陣134
4.7.1逆矩陣的存在性134
4.7.2逆矩陣的定義135
4.7.3初等行矩陣求逆矩陣137
4.7.4高斯若爾當求逆矩陣137
4.7.5逆矩陣的性質138
4.8初等變換求秩139
4.8.1初等行變換求秩139
4.8.2初等列變換與標準形142
4.9分塊矩陣143
4.9.1分塊矩陣的定義143
4.9.2分塊矩陣的運算規則144
4.9.3分塊對角矩陣146
4.9.4分塊矩陣的轉置148
4.9.5西爾維斯特不等式148
第5章線性方程組的解150
5.1解的存在性150
5.2解的個數154
5.2.1解的個數的矩陣觀點155
5.2.2滿秩矩陣有唯一解156
5.3解集157
5.3.1齊次線性方程組的解集157
5.3.2非齊次線性方程組的解161
5.3.3解集的結構164
5.4秩零定理166
5.4.1二維中的例子166
5.4.2三維中的例子167
5.4.3秩零定理的嚴格形式169
第6章行列式170
6.1行列式的來歷170
6.1.1二階行列式171
6.1.2三階行列式172
6.1.3克拉默法則174
6.1.4全排列與逆序數176
6.1.5行列式的定義178
6.2二階行列式179
6.2.1伸縮比例179
6.2.2原理182
6.2.3總結186
6.3向量積187
6.3.1三維空間中的有向面積187
6.3.2向量積的方向188
6.3.3求解三維空間中的有向面積190
6.4三階行列式195
6.4.1有向體積195
6.4.2有向體積之比196
6.4.3總結200
6.5子式和餘子式200
6.5.1子式201
6.5.2餘子式202
6.5.3代數餘子式203
6.5.4總結204
6.6行列式的性質204
6.6.1轉置行列式204
6.6.2滿秩、可逆與行列式205
6.6.3行列式的數乘206
6.6.4行(列)互換207
6.6.5行列式的倍加208
6.6.6行列式的加法210
6.6.7行列式的乘法211
6.6.8三角行列式的計算法212
6.6.9三角分塊行列式的計算法213
6.6.10拉普拉斯展開214
6.6.11拉普拉斯展開的推論217
6.7克拉默法則218
6.8行列式的應用221
6.8.1範德蒙行列式221
6.8.2伴隨矩陣與逆矩陣224
6.8.3伴隨矩陣的秩225
第7章相似矩陣227
7.1函數的坐標系227
7.1.1日心說與地心說227
7.1.2阿基米德螺線228
7.1.3亮度調整229
7.2基變換230
7.2.1各種基變換的例題230
7.2.2過渡矩陣和基變換公式235
7.3座標變換237
7.3.1座標變換公式237
7.3.2矩陣函數和座標變換241
7.4相似矩陣242
7.4.1相似矩陣的定義243
7.4.2相似矩陣的性質247
7.4.3亮度的調整249
第8章特徵向量與對角化252
8.1特徵值與特徵向量252
8.1.1特徵值與特徵向量的定義253
8.1.2特徵空間與特徵方程254
8.1.3互异特徵值對應的特徵向量260
8.2對角化261
8.3再談特徵值與特徵向量265
8.4正交矩陣268
8.4.1正交基269
8.4.2正交矩陣的定義271
8.5施密特正交化273
8.5.1二維空間的正交基274
8.5.2三維空間的正交基276
8.5.3施密特正交化的完整形式279
8.6正交對角化279
8.6.1整體的思路280
8.6.2實對稱陣281
8.6.3完整的解題過程282
8.6.4正交對角化的定義284
8.7相似矩陣中的不變數285
8.7.1相似矩陣的特徵值相同285
8.7.2相似矩陣的行列式相同288
8.7.3相似矩陣的迹相同290
第9章二次型與契约矩陣292
9.1二次型292
9.1.1二次型的定義292
9.1.2從二次型到矩陣293
9.2契约矩陣296
9.2.1契约矩陣的定義299
9.2.2一點補充299
9.3契约對角化300
9.3.1正交契约對角化300
9.3.2拉格朗日配方法303
9.4慣性定理與正負定309
9.4.1慣性定理309
9.4.2正定與負定311







NT$1399
【圖神經網路:基礎、前沿與應用】

NT$1850
6月新書【程式設計不難:全彩圖解+微課+ Python程式設計】

NT$2850
MIT教材:【概率導論+概率論及其應用(卷1+2)+伊藤清概率論】

NT$1480
【視覺化微分幾何和形式】(一部五幕數學正劇)

NT$2400
【量子比特+量子計算+量子佯謬+通幽洞微+萬物一弦+極寒之地】

NT$1680
【矩陣力量:線性代數全彩圖解:微課+Python程式設計】

NT$2800
新版劍橋實用專業英語:【醫學、法律、工程、金融財務、管理、市場行銷】

NT$3150
【量子力學:對稱性第2版】+【量子色動力學第3版】+【場量子化】

NT$1950
【凝聚態物理學】(上下兩卷)

NT$1900
【顛覆性的生物藝術】+【未來藝術在科技奇點衝擊下的蛻變】

NT$3500
【萬物皆數學-用高級的方式理解這個世界】(套裝8冊)

NT$4800
微分幾何與拓撲學:【代數拓撲同調論】+【同倫論】+【古典微分幾何】+【近代微分幾何】+【微分拓撲】

NT$3300
數學領域經典著作:【基礎拓撲學/純數學教程/不等式/矩陣計算/複分析:可視化方法/伊藤清概率論】

NT$2500
【馬祖爾物理學:原理篇+實踐篇】(英文影印版)

NT$2299
【數學物理方法】+【量子力學I】+【量子力學Ⅱ】(全新塑封三册)

NT$2560
【粒子物理學中的規範理論實用導論 】(第1卷+第2卷)

NT$2700
【化學生物學】+【生物信息學與功能基因組學(原著第三版)】(全新塑封兩冊)

NT$1650
【程序員的數學】+【概率統計】+【線性代數】

NT$1400
【力學導論】(軟裝圖片黑白版)

NT$1499
幾何瑰寶:【平面幾何500名題暨1500條定理】(上下册)